Bienvenue dans l’univers captivant de l’écriture des mathématiques en ligne, où les symboles et les expressions prennent vie sur les forums et les réseaux sociaux dédiés à l’éducation comme sur le site web communautaire éducatif Tchad Éducation (https://tchadeducation.com/).
Fondamentalement, lorsqu’on rédige un texte à l’aide d’un ordinateur ou d’un smartphone, on ne dispose pas des symboles et de la mise en forme nécessaire pour exprimer tous les concepts mathématiques. Par exemple, il est ennuyeux d’écrire une fraction ou la racine carrée d’un nombre. Une possibilité est d’écrire : 1/2 pour un demi et V2 pour la racine carrée de 2 ; alors que l’idéal est d’écrire : $\dfrac{1}{2}$ et $\sqrt{2}$. Grâce à des outils tels que MathJax/LaTex, il est possible de communiquer ses idées mathématiques de manière claire et élégante sur le web.
Dans cet article, nous donnons les éléments de base pour commencer rapidement à écrire des mathématiques en ligne, en mettant l’accent sur la manière de tirer parti des fonctionnalités de notre plateforme : le réseau social intégré dans lequel il est possible d’y publier les maths de manière dynamique, c’est-à-dire qu’en cliquant le buton Publier la note, vous voyez immédiatement les rendus mathématiques de votre note, les forums de partage et d’entraide et la rédaction des articles de blogue (pour les membres qui aimeraient devenir des auteurs).
Comment faire afficher les mathématiques en ligne
Notons que les sites ou applications web n’affichent pas tous les symboles et expressions mathématiques, moins encore dynamiquement, tant que les fonctionnalités ne sont pas ajoutées. C’est le cas par exemple des réseaux sociaux célèbres comme Facebook, WhatsApp, Telegram, YouTube pour ne citer que ceux-là. Sur cette plateforme, nous l’avons fait.
Ici, pour qu’un symbole, une formule ou une expression mathématique s’affiche, le code doit toujours être mis entre deux symboles : $...$, \(...\), $$...$$ ou encore \[...\] . Nous donnerons juste ci-dessous la différences de ces quatre formes d’écritures.
Pour écrire au sein d’une phrase, on utilise $...$ ou \(...\). Les écritures $$...$$ et \[...\] affichent hors des textes. Par exemple la phrase :
L’expression $\sum_{i=1}^n i=\frac{n(n+1)}{2}$ est la somme de n premiers entiers naturels non nuls donne :
L’expression $\sum_{i=1}^n i=\frac{n(n+1)}{2}$ est la somme de n premiers entiers naturels non nuls.
Alors que : L’expression $$\sum_{i=1}^n i=\frac{n(n+1)}{2}$$ est la somme de n premiers entiers naturels non nuls donne :
L’expression \[\sum_{i=1}^n i=\frac{n(n+1)}{2}\] est la somme de n premiers entiers naturels non nuls.
Dans les sections qui suivent, nous donnons les syntaxes de base vous permettant de publier très rapidement les mathématiques en ligne.
Exposant, indice, fraction et radical
On utilise respectivement ^, _, \sqrt{...} et \frac{...}{...}.
Ainsi $x^2$, $x_2$, $\sqrt{x}$ et $\frac{1}{2}$ donne respectivement $x^2$, $x_2$, $\sqrt{x}$ et $\frac{1}{2}.$
Si les exposants et les indices sont constitués de plus d’un caractère, les syntaxes les écrivant sont suivis des accolades : ^{...} et _{...}. Nous avons la phrase suivante :
Si $u_n=3^n$ alors $u_{n+1}=3^{n+1}$. Elle s’affiche : Si $u_n=3^n$ alors $u_{n+1}=3^{n+1}.$
Ensembles de nombres
Pour écrire les ensembles des nombres on utilise \mathbb{...} ou juste \mathbb ... sans accolade. Ainsi, $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{D}$, $\mathbb{Q}$, $\mathbb{R}$, $\mathbb{C}$, $\mathbb{H}$, etc. donne respectivement $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{D}$, $\mathbb{Q}$, $\mathbb{R}$, $\mathbb{C}, \mathbb{H}$, etc.
Nous avons simplifié ici la façon d’écrire les ensembles : on peut simplement écrire $\N$, $\Z$, $\D$, $\Q$, $\R$ et $\C$ pour afficher ces mêmes ensembles.
Parenthèse, crochet, accolade
Pour utiliser la parenthèse, le crochet et l’accolade on utilise respectivement (...), [...], \{...\}.
Par exemple $[1 ; 2]=\{x\in \mathbb{R} | 1\leq x \leq 2 \}$ donne $[1 ; 2]=\{x\in \R |1\leq x \leq 2 \} $.
Pour ajuster ces symboles à la taille de toutes les formules, on utilise respectivement \left(...\right), \left[...\right] et \left\{...\right\}
Ainsi \[\{x\in \mathbb{R} \mid \frac{1}{2} \leq x \leq \frac{1}{3} \}\] et \[(\frac{1}{2} +\frac{1}{3})(\frac{1}{2} - \frac{1}{3})=\frac{5}{36}\] donne \[\{x\in \R \mid \frac{1}{2} \leq x \leq \frac{1}{3} \}\] et \[( \frac{1}{2} +\frac{1}{3} )( \frac{1}{2} – \frac{1}{3} )=\frac{5}{36}\]
Alors que: \[\left\{x\in et \mathbb{R} \mid \frac{1}{2} \leq x \leq \frac{1}{3} \right\}\]\[\left( \frac{1}{2} +\frac{1}{3} \right)\left( \frac{1}{2} - \frac{1}{3} \right)=\frac{5}{36}\] donne \[\left\{x\in \R \mid \frac{1}{2} \leq x \leq \frac{1}{3} \right\}\] et \[\left( \frac{1}{2} +\frac{1}{3} \right)\left( \frac{1}{2} – \frac{1}{3} \right)=\frac{5}{36}\]
Module, norme, vecteur, barre, angle
Valeur absolue et module : |...| et \left|...\right| pour ajuster la taille aux formules\[|1+i|=\sqrt{2},\quad \left|\frac{1}{2} + i\frac{\sqrt{3}}{2}\right|=1\] donne \[|1+i|=\sqrt{2},\quad \left|\frac{1}{2} + i\frac{\sqrt{3}}{2}\right|=1\]
Norme : || ... || ou \Vert ... \Vert. Le dernier symbole convient mieux.
Vecteur : \overrightarrow{ ... } \[\Vert \overrightarrow{AB} \Vert = \sqrt{(x_B-x_A)^2+ (y_B-y_A)^2 }\] donne \[\left\Vert \overrightarrow{AB} \right\Vert = \sqrt{(x_B-x_A)^2+ (y_B-y_A)^2 }\]
Barre : \bar{ ... }, \overline{ ... }. Le dernier s’adapte à toutes les lettres.\[\bar{j}=-\frac{1}{2}-i\frac{\sqrt{3}}{2}, \quad \overline{AB}=x_B-x_A\] donne \[\bar{j}=-\frac{1}{2}-i\frac{\sqrt{3}}{2}, \quad \overline{AB}=x_B-x_A\]
Appartenance, inclusion, ensemble vide, union, intersection
Appartenance : \in, (\notin pour la non appartenance)
Inclusion : \subset
Ensemble vide : \emptyset
Union : \cup
Intersection : \cap\[\sqrt{2}\in\mathbb{R}, \quad \sqrt{2}\notin donne \[\sqrt{2}\in\R, \quad \sqrt{2}\notin\Q, \quad \N \subset \Z\] \[ \R_{+}\cup\R_{-}=\R, \quad \R_{+}^{\star}\cap\R_{-}=\emptyset\] \mathbb{Q} , \quad \mathbb{N} \subset \mathbb{Z} \] \[ \mathbb{R}_{+}\cup\mathbb{R}_{-}= \mathbb{R} , \quad \mathbb{R_{+}^{\star}\cap \mathbb{R}_{-}=\emptyset\]
Somme, produit, limite, intégrale, fonction
Somme : \sum_{...}^{...}
\[\sum_{i=1}^n i=\frac{n(n+1)}{2}\] donne \[\sum_{i=1}^n i=\frac{n(n+1)}{2}\]
Produit : \prod_{...}^{....} \[\prod_{k=1}^n k = n!\] donne \[\prod_{k=1}^n i = n!\]
Limite : \lim_{... \to ... } donne \[e^x=\lim_{n\to\infty} \left( 1+\frac{x}{n} \right)^n\]
\[e^x=\lim_{n\to\infty} \left( 1+\frac{x}{n} \right)^n\]
Intégrale : \int_{...}^{...} donne \[\int_{-\infty}^{+\infty} e^{-x^2}{\rm d}x = \sqrt{\pi}\]
\[\int_{-\infty}^{+\infty} e^{-x^2}{\rm d}x = \sqrt{\pi}\]
Fonctions : \sin \arcsin \cos \arcsos \tan \arctan \ln \log \lim \min \max \inf \sup …
Quantificateurs et quelques symboles
Pour tout : \forall
Il existe : \exists
Implique : \Rightarrow (court), \Longrightarrow (long), \implies
Si, et seulement si : \iff
Associe : \mapsto
Supérieur/Inférieur ou égal à : \geq/\leq
Non égal à : \neq ou \ne
Multiplié par : \times
Privé de : \setminus
Infini : \infty
Espaces : \, , \; , ~ , \quad , \qquad
$\forall\epsilon>0\; \exists N\in donne $\forall\epsilon>0 \; \exists N\in \N$ $\forall(p, n)\in \N^2$ $(p\geq N\; n\geq N \Rightarrow\vert u_p-u_n\vert<\epsilon)$. \mathbb{N} $ $\forall(p, n)\in \mathbb{N}^2$ $(p\geq N\; n\geq N \Rightarrow\vert u_p-u_n\vert<\epsilon)$
Alphabet grec
Lettre minuscule : \alpha, \beta, \gamma, \delta, …, \omega
Lettre majuscule : \Alpha, \Beta, \Gamma, \Delta, …, \Omega
$\alpha, \beta, \gamma, \delta, …, \omega$ donne $\alpha, \beta, \gamma, \delta, …, \omega $
De même $\Gamma, \Delta, …, \Omega$ donne $ \Gamma, \Delta, …, \Omega$
Quelques lettres ont des variantes telles : \varepsilon pour \epsilon, \varphi pour \phi, etc. $\epsilon$ : $\epsilon$ $\varepsilon$: $\varepsilon$ $\phi$ : $\phi$ $\varphi$ : $\varphi$
Systèmes d’équations
On peut utiliser \begin{array}…\end{array} et \left\{…\right. ou \begin{cases}…\end{cases}
$$ \left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{array} \right. $$
ou
$$\begin{cases}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{cases} $$
donne
$$\begin{cases}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{cases} $$
Nous allons nous arrêter ici pour le moment. Nous espérons que cet petit guide vous permettra d’écrire les maths sur Tchad Éducation et répondra aux soucis des utilisateurs qui se demandaient comment écrire les mathématiques en ligne.
Pour approfondir le sujet, veuillez vous rendre sur cette page qui peut être considérée comme une référence et sur laquelle vous pouvez copier et adapter quelques codes. Les utilisateurs qui trouveront un peu difficile l’usage de MathJax/Latex peuvent se servir de cet outil, qui peut leur générer des codes Latex. Ils peuvent ensuite faire des copier/coller. Celui-ci est également utile et peut, comme le premier d’ailleurs, être utilisé pour tester les codes Latex que nous donnons ici. Vous pouvez aussi faire usage d’une formule qui a été déjà publié en faisant un clic droit sur l’expression et choisir Show Math AS › TeX Commands.

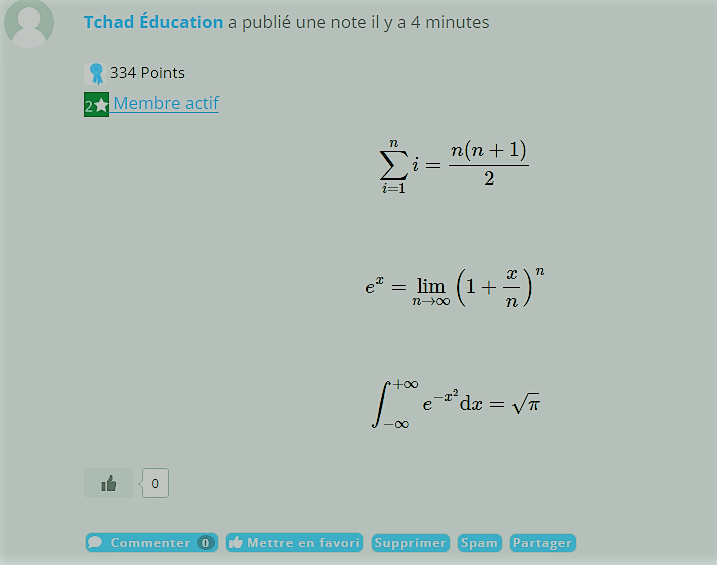

Waouh c’est super. J’aimerai contribuer. $$\sqrt{9} = 3 $$
Nous vous souhaitons la bienvenue ! N’hésitez pas à nous faire savoir votre potentielle contribution.
Waouh. ça fonctionne très bien. A bientôt.
Merci d’avoir essayé !