-
djintelbe a adressé une note au groupe
Les maths pour tous il y a 2 ans et 9 mois · 
10457
Points
Quelques limites usuelles :
$\lim_{x\to 0} \frac{\ln(1+x)}{x}=1$, $\lim_{x\to 0} \frac{\text{e}^x-1}{x}=1$ etc.
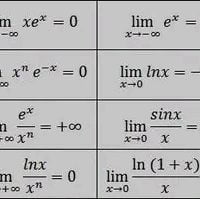
Pour les limites écrites ci-dessus, la preuve est simple. C’est la limite en 0 du taux de variations $\frac{f(x)-f(x_0)}{x-x_0}$ qui vaut $f^\prime(x_0)$, appliqués aux fonctions $x\mapsto \ln(1+x)$ et $x\mapsto \text{e}^x$.
Il en est de même pour les limites
\[\lim_{x\to 0}\frac{\sin x}{x}=1 \; \,\text{et}\] \[\lim_{x\to 0}\frac{1-\cos x}{x}=0.\] Les fonctions correspondantes étant respectivement les fonctions $x\mapsto \sin x$ et $x\mapsto \cos x$.
Utile pour les terminalistes ! Retenez ces limites de référence.